| 副目次 |
|
第 3 章 線形モデルによる生態系分析 1 節 線形モデルの可能性と必要性 2 節 生産者−分解者モデル 3 節 分解者間の競争と共存 4 節 最大呼吸構成の安定性 5 節 モデルの一般化と基本定理 |
| 副目次 |
|
第 3 章 線形モデルによる生態系分析 1 節 線形モデルの可能性と必要性 2 節 生産者−分解者モデル 3 節 分解者間の競争と共存 4 節 最大呼吸構成の安定性 5 節 モデルの一般化と基本定理 |
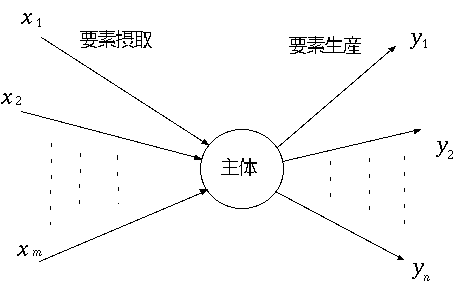
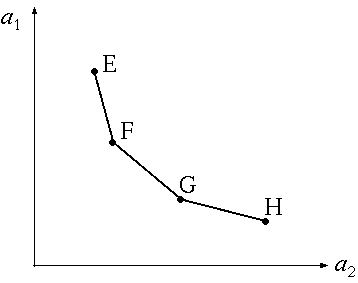
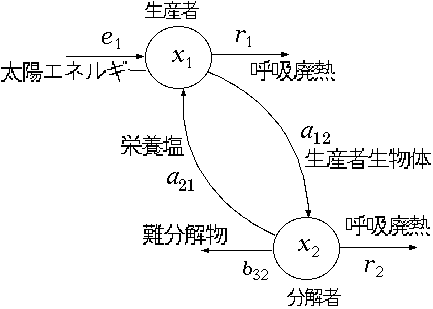
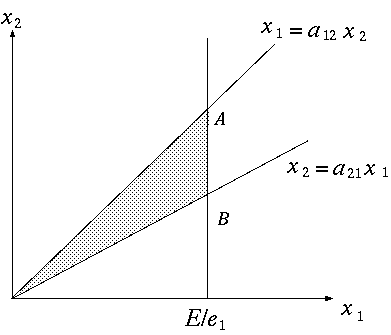

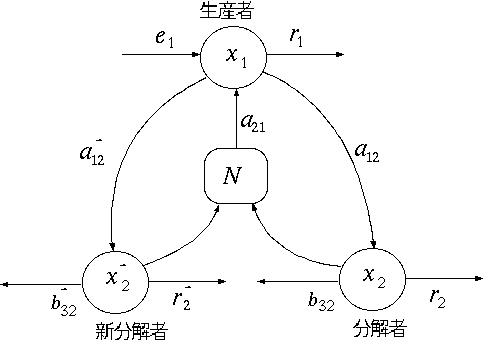
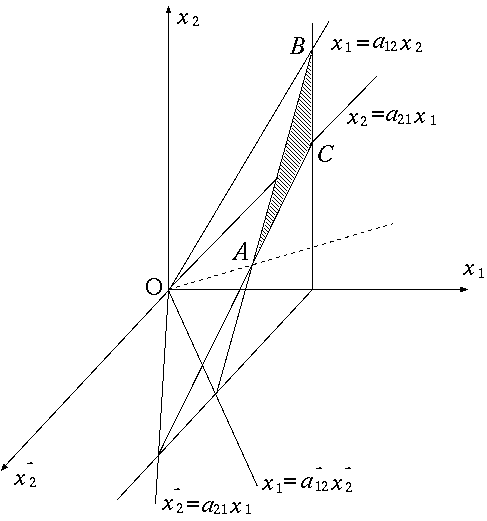
 , p.156。(もどる)
, p.156。(もどる) 。(もどる)
。(もどる) , Finn~
, Finn~ , Hannon~
, Hannon~ , Constanza~
, Constanza~ , Herendeen~
, Herendeen~ , Constanza and Herendeen~
, Constanza and Herendeen~ , Constanza and Hannon~
, Constanza and Hannon~ , Hannon~
, Hannon~ など。(もどる)
など。(もどる) 。(もどる)
。(もどる) , Morishima~
, Morishima~ 。(もどる)
。(もどる) 。(もどる)
。(もどる) 。(もどる)
。(もどる) 。(もどる)
。(もどる) , p.49。(もどる)
, p.49。(もどる)