| 副目次 |
|
第 4 章 生態系モデルのシミュレーション 1 節 モデル生態系の構造 2 節 最大呼吸問題の定式化 3 節 最大呼吸解としての群集構成 4 節 双対解と呼吸廃熱価値体系 5 節 群集構成の最適性と現実性 |
| 副目次 |
|
第 4 章 生態系モデルのシミュレーション 1 節 モデル生態系の構造 2 節 最大呼吸問題の定式化 3 節 最大呼吸解としての群集構成 4 節 双対解と呼吸廃熱価値体系 5 節 群集構成の最適性と現実性 |
| 植食 | 肉食 | 微生物食 | 腐食 | |||||
| A/C | P/A | A/C | P/A | A/C | P/A | A/C | P/A | |
| 微生物 | --- | --- | --- | --- | --- | --- | --- | 0.40 |
| 無脊椎動物 | 0.40 | 0.40 | 0.80 | 0.30 | 0.30 | 0.40 | 0.20 | 0.40 |
| 脊椎恒温動物 | 0.50 | 0.02 | 0.80 | 0.02 | --- | --- | --- | --- |
| 脊椎変温動物 | 0.50 | 0.10 | 0.80 | 0.10 | --- | --- | --- | --- |
| 主体 | 要素 | ||||
| 名前 | 名前 | ||||
| 1 | P | 植物 | 1 | S | 太陽光 |
| 2 | Ha | 植食動物(恒温) | 2 | N | 栄養塩 |
| 3 | Hb | 植食動物(変温) | 3 | Hu | 腐植・難分解物 |
| 4 | Hc | 植食動物(無脊椎) | 4 | Pv | 植物体(脊椎動物) |
| 5 | Cga | 肉食動物(恒温,生食系) | 5 | Pi | 植物体(無脊椎動物) |
| 6 | Cgb | 肉食動物(変温,生食系) | 6 | Bpv | 植食動物体(脊椎) |
| 7 | Cgc | 肉食動物(無脊椎,生食系) | 7 | Bpi | 植食動物体(無脊椎) |
| 8 | Mfc | 微生物(肉食動物排泄物) | 8 | Bc | 肉食動物体 |
| 9 | Sfc | 腐食動物(肉食動物排泄物) | 9 | Bs | 腐食動物体 |
| 10 | Mfo | 微生物(一般排泄物) | 10 | Bm | 微生物食動物体 |
| 11 | Sfo | 腐食動物(一般排泄物) | 11 | M | 微生物体 |
| 12 | Mp | 微生物(植物遺体) | 12 | Fc | 排泄物(肉食動物) |
| 13 | Sp | 腐食動物(植物遺体) | 13 | Fo | 排泄物(一般) |
| 14 | Ma | 微生物(動物遺体) | 14 | Dp | 植物遺体 |
| 15 | Sa | 腐食動物(動物遺体) | 15 | Da | 動物遺体 |
| 16 | Im | 微生物食動物 | R | 呼吸廃熱 | |
| 17 | Csa | 肉食動物(恒温,腐食系) | |||
| 18 | Csb | 肉食動物(変温,腐食系) | |||
| 19 | Csc | 肉食動物(無脊椎,腐食系) | |||
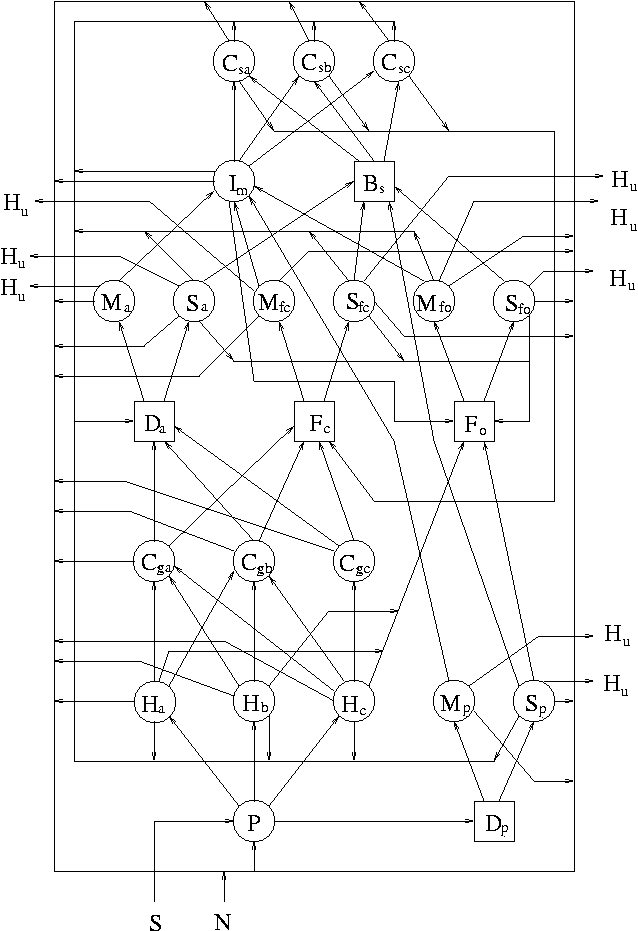
| P | Ha | Hb | Hc | Cga | Cgb | Cgc | Mfc | Sfc | ||
| 1 | S | 50.0 | --- | --- | --- | --- | --- | --- | --- | --- |
| 2 | N | 0.6 | --- | --- | --- | --- | --- | --- | --- | --- |
| 3 | Hu | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 4 | Pv | --- | 1.0 | 1.0 | --- | --- | --- | --- | --- | --- |
| 5 | Pi | --- | --- | --- | 1.0 | --- | --- | --- | --- | --- |
| 6 | Bpv | --- | --- | --- | --- | 0.8 | 0.7 | --- | --- | --- |
| 7 | Bpi | --- | --- | --- | --- | 0.2 | 0.3 | 1.0 | --- | --- |
| 8 | Bc | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 9 | Bs | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 10 | Bm | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 11 | M | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 12 | Fc | --- | --- | --- | --- | --- | --- | --- | 1.0 | 1.0 |
| 13 | Fo | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 14 | Dp | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 15 | Da | --- | --- | --- | --- | 1.0 | 1.0 | 1.0 | --- | --- |
| Mfo | Sfo | Mp | Sp | Ma | Sa | Im | Csa | Csb | Csc | |
| S | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| N | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Hu | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Pv | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Pi | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Bpv | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Bpi | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Bc | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Bs | --- | --- | --- | --- | --- | --- | --- | 0.5 | 0.6 | 0.7 |
| Bm | --- | --- | --- | --- | --- | --- | --- | 0.5 | 0.4 | 0.3 |
| M | --- | --- | --- | --- | --- | --- | 1.0 | --- | --- | --- |
| Fc | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Fo | 1.0 | 1.0 | --- | --- | --- | --- | --- | --- | --- | --- |
| Dp | --- | --- | 1.0 | 1.0 | --- | --- | --- | --- | --- | --- |
| Da | --- | --- | --- | --- | 1.0 | 1.0 | --- | 1.0 | 1.0 | 1.0 |
| P | Ha | Hb | Hc | Cga | Cgb | Cgc | Mfc | Sfc | ||
| 1 | S | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 2 | N | --- | 0.06 | 0.03 | 0.01 | 0.200 | 0.10 | 0.05 | 2.400 | 1.800 |
| 3 | Hu | --- | --- | --- | --- | --- | --- | --- | 0.008 | 0.016 |
| 4 | Pv | 0.150 | --- | --- | --- | --- | --- | --- | --- | --- |
| 5 | Pi | 0.024 | --- | --- | --- | --- | --- | --- | --- | --- |
| 6 | Bpv | --- | 0.01 | 0.05 | --- | --- | --- | --- | --- | --- |
| 7 | Bpi | --- | --- | --- | 0.16 | --- | --- | --- | --- | --- |
| 8 | Bc | --- | --- | --- | --- | 0.016 | 0.08 | 0.24 | --- | --- |
| 9 | Bs | --- | --- | --- | --- | --- | --- | --- | --- | 0.080 |
| 10 | Bm | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 11 | M | --- | --- | --- | --- | --- | --- | --- | 0.392 | --- |
| 12 | Fc | --- | --- | --- | --- | 0.200 | 0.20 | 0.20 | --- | --- |
| 13 | Fo | --- | 0.50 | 0.50 | 0.60 | --- | --- | --- | --- | 0.784 |
| 14 | Dp | 0.426 | --- | --- | --- | --- | --- | --- | --- | --- |
| 15 | Da | --- | 0.01 | 0.05 | 0.16 | 0.016 | 0.08 | 0.24 | --- | 0.080 |
| R | 0.4 | 0.49 | 0.45 | 0.24 | 0.784 | 0.72 | 0.56 | 0.6 | 0.120 |
| Mfo | Sfo | Mp | Sp | Ma | Sa | Im | Csa | Csb | Csc | |
| S | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| N | 0.800 | 0.400 | 0.30 | 0.10 | 0.400 | 0.200 | 0.10 | 0.200 | 0.10 | 0.05 |
| Hu | 0.016 | 0.032 | 0.04 | 0.08 | 0.032 | 0.064 | --- | --- | --- | --- |
| Pv | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Pi | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Bpv | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Bpi | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Bc | --- | --- | --- | --- | --- | --- | --- | 0.016 | 0.08 | 0.24 |
| Bs | --- | 0.080 | --- | 0.08 | --- | 0.080 | --- | --- | --- | --- |
| Bm | --- | --- | --- | --- | --- | --- | 0.12 | --- | --- | --- |
| M | 0.384 | --- | 0.36 | --- | 0.368 | --- | --- | --- | --- | --- |
| Fc | --- | --- | --- | --- | --- | --- | --- | 0.200 | 0.20 | 0.20 |
| Fo | --- | 0.768 | --- | 0.72 | --- | 0.736 | 0.70 | --- | --- | --- |
| Dp | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Da | --- | 0.080 | --- | 0.08 | --- | 0.080 | 0.12 | 0.016 | 0.08 | 0.24 |
| R | 0.6 | 0.120 | 0.6 | 0.12 | 0.6 | 0.120 | 0.18 | 0.784 | 0.72 | 0.56 |
| No. | 主体 | 活動水準 | 生産 | 排泄 | 腐植 | 栄養塩 | 呼吸廃熱 |
| 1 | P | 166.6667 | 100.0000 | --- | --- | --- | 66.6667 |
| 2 | Ha | --- | --- | --- | --- | --- | --- |
| 3 | Hb | 25.0000 | 1.2500 | 12.5000 | --- | 0.7500 | 11.2500 |
| 4 | Hc | 4.0000 | 0.6400 | 2.4000 | --- | 0.0400 | 0.9600 |
| 5 | Cga | 1.5625 | 0.0250 | 0.3125 | --- | 0.3125 | 1.2250 |
| 6 | Cgb | --- | --- | --- | --- | --- | --- |
| 7 | Cgc | 0.3275 | 0.0786 | 0.0655 | --- | 0.0164 | 0.1834 |
| 8 | Mfc | 2.8820 | 1.1297 | --- | 0.0231 | 6.9168 | 1.7292 |
| 9 | Sfc | --- | --- | --- | --- | --- | --- |
| 10 | Mfo | 83.8608 | 32.2025 | --- | 1.3418 | 67.0886 | 50.3165 |
| 11 | Sfo | 32.6663 | 2.6133 | --- | 1.0453 | 13.0665 | 3.9200 |
| 12 | Mp | --- | --- | --- | --- | --- | --- |
| 13 | Sp | 71.0000 | 5.6800 | 51.1200 | 5.6800 | 7.1000 | 8.5200 |
| 14 | Ma | --- | --- | --- | --- | --- | --- |
| 15 | Sa | 2.8353 | 0.2268 | 2.0868 | 0.1815 | 0.5671 | 0.3402 |
| 16 | Im | 33.3323 | 3.9999 | 23.3326 | --- | 3.3332 | 5.9998 |
| 17 | Csa | 1.2194 | 0.0195 | 0.2439 | --- | 0.2439 | 0.9560 |
| 18 | Csb | --- | --- | --- | --- | --- | --- |
| 19 | Csc | 11.3006 | 2.7122 | 2.2601 | --- | 0.5650 | 6.3284 |
| 脊椎動物 | 0.04 | |
| 哺乳類 | 0.01 | |
| 鳥類 | 0.03 | |
| その他 | ? | |
| 地上無脊椎動物 | 2.64 | |
| 地上動物計 | 2.68 | |
| 線虫 | 30.36 | |
| 節足動物 | 5.95 | |
| 環形動物 | 7.35 | |
| 原生動物 | 0.69 | |
| 土壌動物計 | 44.35 | |
| 酵母 | 0.07 | |
| 菌類 | 1770.6 | |
| 細菌 | 463.8 | |
| 土壌微生物計 | 2234.5 | |
| 価値損失 | 呼吸廃熱価値 | ||||
| No. | 記号 | No. | 記号 | ||
| 1 | P | --- | 1 | S | 0.01901 |
| 2 | Ha | 0.000034 | 2 | N | 0.14989 |
| 3 | Hb | --- | 3 | Hu | --- |
| 4 | Hc | --- | 4 | Pv | 1.08888 |
| 5 | Cga | --- | 5 | Pi | 1.11363 |
| 6 | Cgb | 0.008923 | 6 | Bpv | 0.02284 |
| 7 | Cgc | --- | 7 | Bpi | 0.02005 |
| 8 | Mfc | --- | 8 | Bc | --- |
| 9 | Sfc | 0.020573 | 9 | Bs | 0.01671 |
| 10 | Mfo | --- | 10 | Bm | 0.02785 |
| 11 | Sfo | --- | 11 | M | 1.13938 |
| 12 | Mp | 0.001766 | 12 | Fc | 1.40636 |
| 13 | Sp | --- | 13 | Fo | 1.15743 |
| 14 | Ma | 0.011170 | 14 | Dp | 1.05691 |
| 15 | Sa | --- | 15 | Da | 1.09042 |
| 16 | Im | --- | |||
| 17 | Csa | --- | |||
| 18 | Csb | 0.008087 | |||
| 19 | Csc | --- | |||
| 栄養塩 | 植物体 | 脊椎恒温 | 一般 | 動物 | 呼吸 | |
| 植食動物体 | 排泄物 | 遺体 | 廃熱 | |||
| 構成 | -0.06 | 1.00 | -0.01 | -0.50 | -0.01 | -0.49 |
| 価値 | 0.145 | 1.089 | 0.023 | 1.157 | 1.090 | 1.00 |
| 価値×構成 | -0.009 | 1.089 | -0.000 | -0.578 | -1.011 | -0.49 |
| No. | 記号 | I | II |
| 総呼吸 | 158.3960 | 158.3964 | |
| 1 | P | 166.6667 | 166.6667 |
| 2 | Ha | 25.0000 | 25.0000 |
| 3 | Hb | --- | --- |
| 4 | Hc | 4.0000 | 4.0000 |
| 5 | Cga | 0.2500 | 0.2500 |
| 6 | Cgb | --- | --- |
| 7 | Cgc | 0.5900 | 0.5900 |
| 8 | Mfc | 2.6696 | 2.6696 |
| 9 | Sfc | --- | --- |
| 10 | Mfo | 83.8491 | 83.9268 |
| 11 | Sfo | 32.6006 | 32.5581 |
| 12 | Mp | --- | --- |
| 13 | Sp | 71.0000 | 71.0000 |
| 14 | Ma | --- | --- |
| 15 | Sa | 2.8821 | 2.8780 |
| 16 | Im | 33.2445 | 33.2744 |
| 17 | Csa | 1.1848 | 1.2029 |
| 18 | Csb | --- | --- |
| 19 | Csc | 11.3232 | 11.3049 |
 。他に Begon~
。他に Begon~ , p.677。(もどる)
, p.677。(もどる) は,多年生草本群落*の総生産の効率を1.3〜1.6\%としている。この効率はここでのモデルのように植物を一つのコンパートメントとしてまとめている状況では,結果に何ら影響を与えないので,わかりやすいように,2.0\%と想定した。また,同じく多年性草本群落の,総生産に対する*純生産の比を0.55〜0.65としているが,ここでは,0.6とした。(もどる)
は,多年生草本群落*の総生産の効率を1.3〜1.6\%としている。この効率はここでのモデルのように植物を一つのコンパートメントとしてまとめている状況では,結果に何ら影響を与えないので,わかりやすいように,2.0\%と想定した。また,同じく多年性草本群落の,総生産に対する*純生産の比を0.55〜0.65としているが,ここでは,0.6とした。(もどる) は植物の乾燥重量*に対する窒素含有量を平均で3\%,同じく脊椎動物平均で10\%であるとしている。陸上植物の乾燥重量1gあたりの平均熱量は4.5kcal,同じく脊椎動物のそれは5.6kcalであるから(たとえばOdum~
は植物の乾燥重量*に対する窒素含有量を平均で3\%,同じく脊椎動物平均で10\%であるとしている。陸上植物の乾燥重量1gあたりの平均熱量は4.5kcal,同じく脊椎動物のそれは5.6kcalであるから(たとえばOdum~ )栄養塩の単位をある程度具体的にとらえることは可能である。(もどる)
)栄養塩の単位をある程度具体的にとらえることは可能である。(もどる) 参照。(もどる)
参照。(もどる) の結果を吉良~
の結果を吉良~ より引用。(もどる)
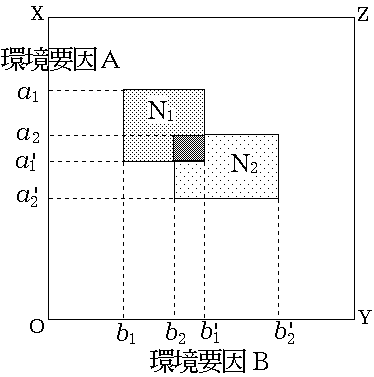
より引用。(もどる) によって与えられたものである。*ニッチ概念の歴史については,マッキントッシュ~
によって与えられたものである。*ニッチ概念の歴史については,マッキントッシュ~ ッキントッシュ89}。他に,ホイッタカー~
ッキントッシュ89}。他に,ホイッタカー~ , Odum~
, Odum~ , 黒岩~
, 黒岩~ など参照。(もどる)
など参照。(もどる) , ホイッタカー~
, ホイッタカー~ , Hutchinson~
, Hutchinson~ など。(もどる)
など。(もどる)